Linear regression is used for finding linear relationship between target and one or more predictors. There are two types of linear regression- Simple and Multiple.

The core idea of Simple Linear Regression is to obtain a line that best fits the data. The best fit line is the one for which total prediction error (all data points) are as small as possible. Error is the distance between the point to the regression line.

Real-time example
We have a dataset which contains information about relationship between ‘number of hours studied’ and ‘marks obtained’. Many students have been observed and their hours of study and grade are recorded. This will be our training data. Goal is to design a model that can predict marks if given the number of hours studied. Using the training data, a regression line is obtained which will give minimum error. This linear equation is then used for any new data. That is, if we give number of hours studied by a student as an input, our model should predict their mark with minimum error.

Y(pred) = b0 + b1*x

The values b0 and b1 must be chosen so that they minimize the error. If sum of squared error is taken as a metric to evaluate the model, then goal to obtain a line that best reduces the error.

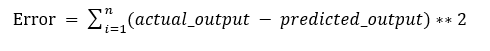If we don’t square the error, then positive and negative point will cancel out each other.

For model with one predictor,



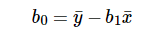
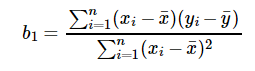
Co-efficient from Normal equations

Apart from above equation co-efficient of the model can also be calculated from normal equation.