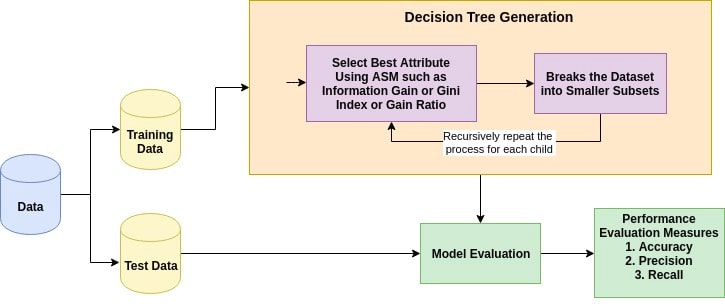
Decision Tree

Decision Tree...

Decision Tree is one of the easiest and popular classification algorithms to understand and interpret. It can be utilized for both classification and regression kind of problem.

Attribute selection measure is a heuristic for selecting the splitting criterion that partition data into the best possible manner. It is also known as splitting rules because it helps us to determine breakpoints for tuples on a given node. ASM provides a rank to each feature(or attribute) by explaining the given dataset. Best score attribute will be selected as a splitting attribute . In the case of a continuous-valued attribute, split points for branches also need to define. Most popular selection measures are Information Gain, Gain Ratio, and Gini Index.

Information gain is the decrease in entropy. Information gain computes the difference between entropy before split and average entropy after split of the dataset based on given attribute values.

Information gain is biased for the attribute with many outcomes. It means it prefers the attribute with a large number of distinct values.

The gain ratio can be defined as:

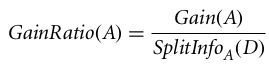
The attribute with the highest gain ratio is chosen as the splitting attribute.

Another decision tree algorithm CART (Classification and Regression Tree) uses the Gini method to create split points.

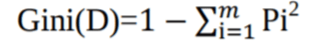
Where, pi is the probability that a tuple in D belongs to class Ci.
The Gini Index considers a binary split for each attribute. You can compute a weighted sum of the impurity of each partition.

criterion : optional (default=”gini”) or Choose attribute selection measure: This parameter allows us to use the different-different attribute selection measure. Supported criteria are “gini” for the Gini index and “entropy” for the information gain.

splitter : string, optional (default=”best”) or Split Strategy: This parameter allows us to choose the split strategy. Supported strategies are “best” to choose the best split and “random” to choose the best random split.

max_depth : int or None, optional (default=None) or Maximum Depth of a Tree: The maximum depth of the tree. If None, then nodes are expanded until all the leaves contain less than min_samples_split samples. The higher value of maximum depth causes overfitting, and a lower value causes underfitting (Source).

1. Decision trees are easy to interpret and visualize.
2. It can easily capture Non-linear patterns.
3. It requires fewer data preprocessing from the user, for example, there is no need to normalize columns.
4. It can be used for feature engineering such as predicting missing values, suitable for variable selection.
5. The decision tree has no assumptions about distribution because of the non-parametric nature of the algorithm.

1. Sensitive to noisy data. It can overfit noisy data.
2. The small variation(or variance) in data can result in the different decision tree. This can be reduced by bagging and boosting algorithms.
3. Decision trees are biased with imbalance dataset, so it is recommended that balance out the dataset before creating the decision tree.