Gradient Descent :
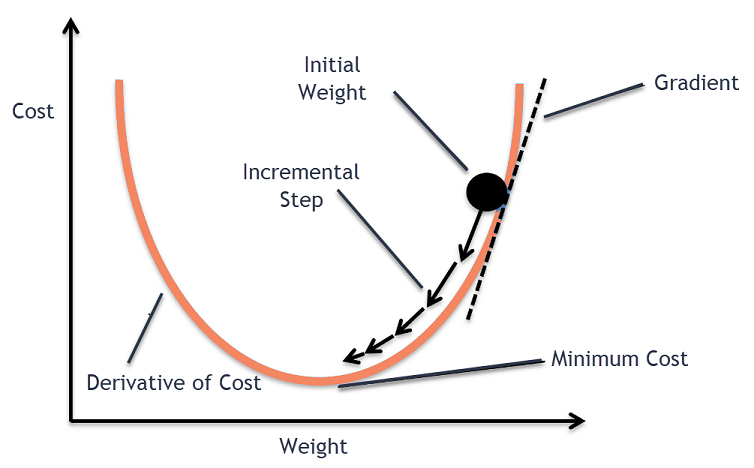
Gradient descent is a first-order iterative optimization algorithm for finding the minimum of a function.
Gradient Descent is a popular optimization technique in Machine Learning and Deep Learning, and it can be used with most
of the learning algorithms. A gradient is the slope of a function. It measures the degree of change of a variable in response
to the changes of another variable. Mathematically, Gradient Descent is a convex function whose output is the partial derivative
of a set of parameters of its inputs. The greater the gradient, the steeper the slope.
Starting from an initial value, Gradient Descent is run iteratively to find the optimal values of the parameters to find the minimum
possible value of the given cost function .
Typically, there are three types of Gradient Descent:
1. Batch Gradient Descent
2. Stochastic Gradient Descent
3. Mini-batch Gradient Descent
Batch Gradient Descent :
In Batch Gradient Descent, all the training data is taken into consideration to take a single step. We take the average of
the gradients of all the training examples and then use that mean gradient to update our parameters. So that’s just one step
of gradient descent in one epoch.
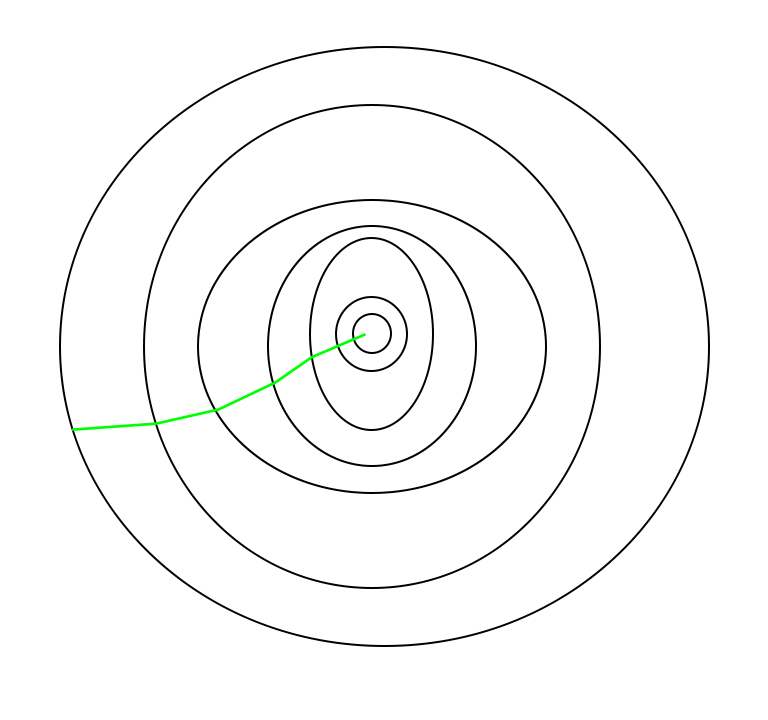
Batch Gradient Descent is great for convex or relatively smooth error manifolds. In this case, we move somewhat directly
towards an optimum solution.
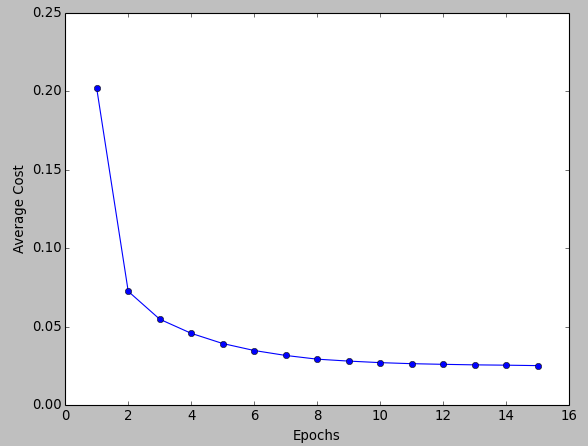
The graph of cost vs epochs is also quite smooth because we are averaging over all the gradients of training data
for a single step. The cost keeps on decreasing over the epochs.
Stochastic Gradient Descent :
In Batch Gradient Descent, we were considering all the samples of the datasets for every step of Gradient Descent. But if our dataset is very huge, this technique does not seem an an efficient way.
To tackle this problem, we have Stochastic Gradient Descent , where a few samples are selected randomly instead of the whole dataset for each iteration.
Now if we drive in more detailed info, in Gradient Descent, there is a term called batch, which denotes the total number of samples from a dataset that is used for calculating the gradient for each iteration. As said
earlier, in typical Gradient Desecnt optimization, like Batch Gradient Descent, the batch is taken to be the whole dataset.
Although, using the whole dataset is really useful for getting to the minima in a less noisy and rendom manner, but the problem arises when our datasets gets big, BGD seems to be an unefficient technique here, performing each iteration on
whole dataset of millions until the minina is reached, definitely it becomes very much expensive to perform.
This problem is solved by Stochastic Gradient Descent(SGD). In SGD, it uses only a single sample, i.e., a batch size of one, to perform each iteration. The sample is randomly shuffled and selected for performing the iteration.
In SGD, since only one sample from the dataset is chosen at random for
each iteration, the path taken by the algorithm to reach the minima is
usually noisier than your typical Gradient Descent algorithm. But that
doesn’t matter as long as we reach the minima and with significantly shorter
training time by using SGD.

Path taken by Batch Gradient Descent :
Path taken by Stochastic Gradient Descent :
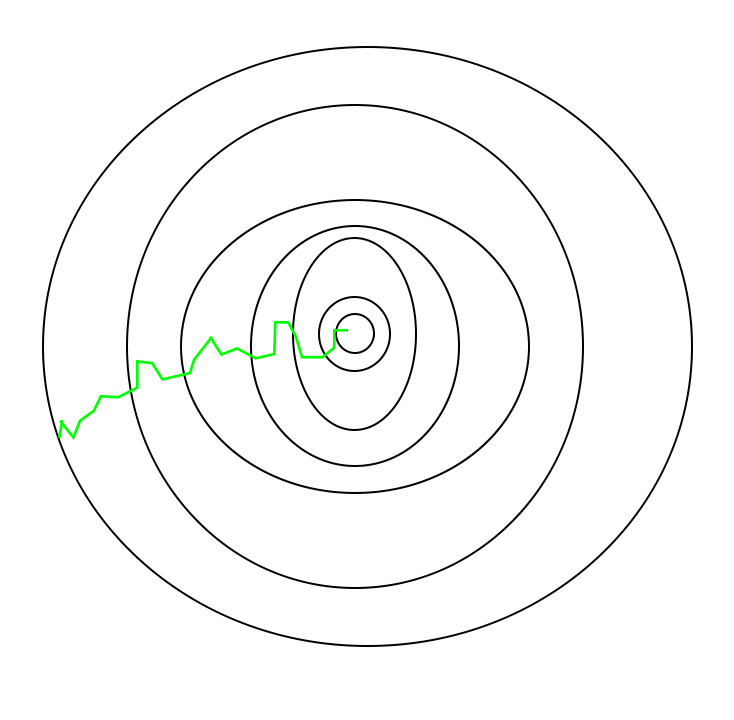
There is a small limitation with SGD, that is SGD is generally noisier than
typical Gradient Descent (GD), it usually took a higher number of iterations
to reach the minima, because of its randomness in its descent.
Even though it requires a higher number of iterations to reach
the minima than typical Gradient Descent, it is still computationally
much less expensive than typical Gradient Descent. Hence, in most
scenarios, SGD is preferred over Batch Gradient Descent for
optimizing a learning algorithm.

This cycle of taking the values and adjusting them based on
different parameters in order to reduce the loss function is
called back-propagation .
Mini Batch Gradient Descent :
Batch Gradient Descent can be used for smoother curves. SGD can be used when the dataset is large. Batch Gradient Descent converges directly to minima. SGD converges faster for larger datasets. But, since in SGD we use only one example at a
time, we cannot implement the vectorized implementation on it. This can slow down the computations. To tackle this problem, a mixture of Batch Gradient Descent and SGD is used.
Here, we use neither all the dataset at once nor we use the single example at a time. We use a batch of a fixed number of training examples which is less than the actual dataset and call it a mini-batch.
So, when we are using the mini-batch gradient descent we are updating our parameters frequently as well as we can use vectorized implementation for faster computations.
Learn More