Clustering can be considered the most important unsupervised learning problem . So, as every other problem of this kind, it deals with finding a structure in a collection of unlabeled data. A loose definition of clustering could be “the process of organizing objects into groups whose members are similar in some way”. A cluster is therefore a collection of objects which are “similar” between them and are “dissimilar” to the objects belonging to other clusters.



Distance-based Clustering :

Given a set of points, with a notion of distance between points, grouping the points into some number of clusters, such that

1. internal (within the cluster) distances should be small i.e members of clusters are close/similar to each other.
2. external (intra-cluster) distances should be large i.e. members of different clusters are dissimilar.

The goal of clustering is to determine the internal grouping in a set of unlabeled data.

Clustering Algorithms : Clustering algorithms may be classified as listed below:

1. Exclusive Clustering
2. Overlapping Clustering
3. Hierarchical Clustering
4. Probabilistic Clustering

Most used clustering algorithms are :
1. K-means
2. Fuzzy K-means
3. Hierarchical clustering
4. Mixture of Gaussians

K-means is an exclusive clustering algorithm, Fuzzy K-means is an overlapping clustering algorithm, Hierarchical clustering is obvious and lastly Mixture of Gaussians is a probabilistic clustering algorithm.

K Means Clustering


Hierarchical clustering (Agglomerative and Divisive clustering) :

hierarchical clustering analysis is a method of cluster analysis which seeks to build a hierarchy of clusters i.e. tree type structure based on the hierarchy.

A Hierarchical clustering method works via grouping data into a tree of clusters. Hierarchical clustering begins by treating every data points as a separate cluster. Then, it repeatedly executes the subsequent steps:
1. Identify the 2 clusters which can be closest together, and
2. Merge the 2 maximum comparable clusters. We need to continue these steps until all the clusters are merged together.

In Hierarchical Clustering, the aim is to produce a hierarchical series of nested clusters. A diagram called Dendrogram (A Dendrogram is a tree-like diagram that statistics the sequences of merges or splits) graphically represents this hierarchy and is an inverted tree that describes the order in which factors are merged (bottom-up view) or cluster are break up (top-down view).

The basic method to generate hierarchical clustering are : Agglomerative and Divisive










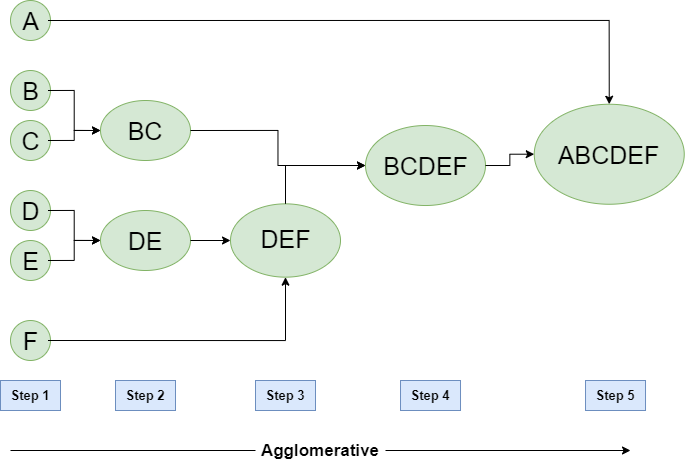
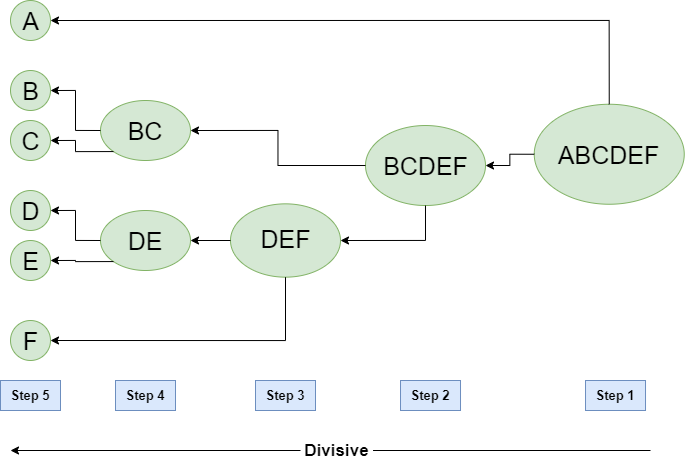
Hierarchical Agglomerative vs Divisive clustering –

1. Divisive clustering is more complex as compared to agglomerative clustering.

2. Divisive clustering is more efficient if we do not generate a complete hierarchy all the way down to individual data leaves.

3. Time complexity of a naive agglomerative clustering is O(n3) but it can be brought down to O(n2). Whereas for divisive clustering given a fixed number of top levels, using an efficient algorithm like K-Means, divisive algorithms are linear in the number of patterns and clusters.

4. Divisive algorithm is also more accurate.